Muster

Ein Muster (engl. pattern) ist eine Kombination von Zahlen, die zu einer eindeutigen (Teil-)Lösung führen. Durch das Merken und Wiedererkennen von Mustern lässt sich die Zeit reduzieren, die zum Nachdenken benötigt wird.

Einfache Muster

	L B1 Wenn eine Zahl dieselbe Anzahl an Zellen berührt, dann sind alle diese Zellen Minen.
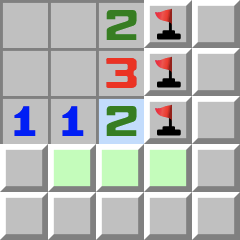	L B2 Wenn eine Zahl dieselbe Anzahl an Minen berührt, dann können alle weiteren angrenzenden Zellen geöffnet werden.
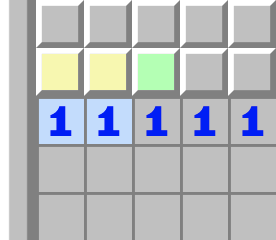	M 1–1 Betrachten Sie die linke 1. Sie berührt die beiden gelben Zellen, weshalb genau eine davon eine Mine ist. Betrachten Sie nun die rechte 1. Sie berührt ebenfalls die beiden gelben Zellen, hat also schon eine Mine, weshalb die grüne Zelle keine Mine mehr sein kann.
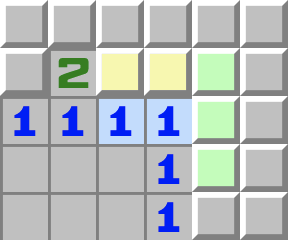	M 1–1+ Betrachten Sie die linke 1. Sie berührt die beiden gelben Zellen, weshalb genau eine davon eine Mine ist. Betrachten Sie nun die rechte 1. Sie berührt ebenfalls die beiden gelben Zellen, hat also schon eine Mine, weshalb keine der grünen Zellen eine Mine sein kann.
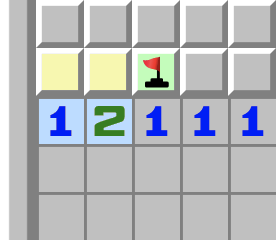	M 1–2 Betrachten Sie die 1. Sie berührt die beiden gelben Zellen, weshalb genau eine davon eine Mine ist. Betrachten Sie nun die 2. Die erste ihrer beiden Minen ist in den gelben Zellen, weshalb die andere Mine in der grünen Zelle sein muss.
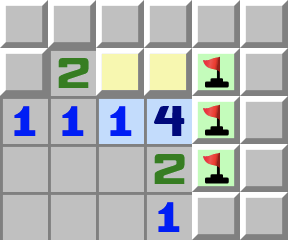	M 1–2+ Betrachten Sie die 1. Sie berührt die beiden gelben Zellen, weshalb genau eine davon eine Mine ist. Betrachten Sie nun die 4. Sie berührt ebenfalls die beiden gelben Zellen, hat also bereits eine Mine. Da nur noch drei weitere Zellen angrenzen, müssen diese allesamt Minen sein.
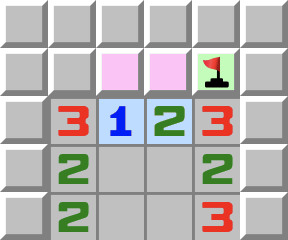	M 1–2C Klassische Version des 1–2 Musters: Betrachten Sie die lila Zellen. Was lässt sich hieraus schließen? Sie können nicht beide Minen sein, weil das der 1 widersprechen würde. Betrachten Sie nun die 2. Wenn die lila Zellen nicht beide Minen sein können, dann muss die übrige grüne Zelle eine Mine sein.
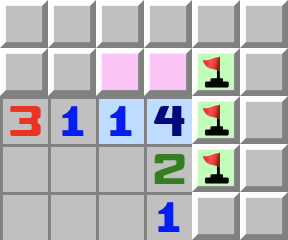	M 1–2C+ Betrachten Sie die lila Zellen. Was lässt sich hieraus schließen? Sie können nicht beide Minen sein, weil das der 1 widersprechen würde. Betrachten Sie nun die 4. Wenn die lila Zellen nicht beide Minen sein können, dann müssen die übrigen drei grünen Zellen allesamt Minen sein.
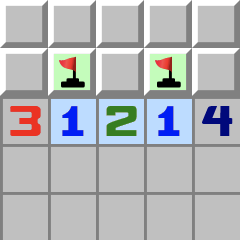	M 1–2–1 Das 1–2–1 Muster hat genau eine Lösung. Genaugenommen ist es nur eine Kombination von zwei 1–2 Mustern: Wenden Sie das 1–2 Muster von links an. Wenden Sie das 1–2 Muster von rechts an. Und hier ist das Ergebnis.
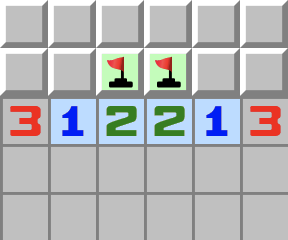	M 1–2–2–1 Das 1–2–2–1 Muster hat genau eine Lösung. Es ist ebenfalls nur eine Kombination von zwei 1–2 Mustern: Wenden Sie das 1–2 Muster von links an. Wenden Sie das 2–1 Muster von rechts an. Und hier ist das Ergebnis.

Reduktion

	S 1–1R 2 wird zur 1, da sie bereits eine Mine hat. 4 wird außerdem zur 1, da sie bereits 3 Minen hat Deshalb wird aus 2–4 durch Reduktion 1–1 und die grüne dritte Zelle kann geöffnet werden.
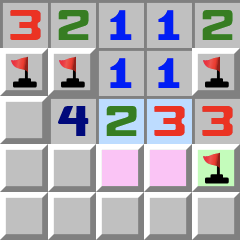	S 1–2R 2 wird zur 1, da sie bereits eine Mine hat. 3 wird ebenfalls zur 2, da sie bereits eine Mine hat. Deshalb wird aus 2–3 durch Reduktion das 1–2 Muster und die grüne dritte Zelle muss eine Mine sein.
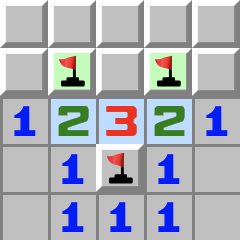	S 1–2–1R 2–3–2 wird zum 1–2–1 Muster.

Löcher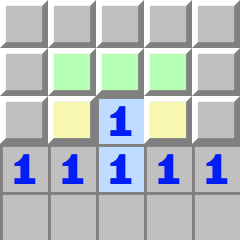

	S H1 Betrachten Sie die untere 1. Sie berührt die beiden gelben Zellen, von denen deshalb genau eine eine Mine ist. Betrachten Sie nun die obere 1. Sie berührt ebenfalls die beiden gelben Zellen, hat also bereits eine Mine, weshalb die übrigen grünen Zellen geöffnet werden können.
	S H2 Betrachten Sie die untere 1. Sie berührt die beiden gelben Zellen, von denen deshalb genau eine eine Mine ist. Betrachten Sie nun die obere 1. Sie berührt ebenfalls die beiden gelben Zellen, hat also bereits eine Mine, weshalb die übrigen grünen Zellen geöffnet werden können.
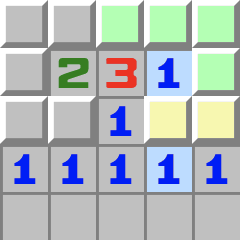	S H3 Betrachten Sie die untere 1. Sie berührt die beiden gelben Zellen, von denen deshalb genau eine eine Mine ist. Betrachten Sie nun die obere 1. Sie berührt ebenfalls die beiden gelben Zellen, hat also bereits eine Mine, weshalb die übrigen grünen Zellen geöffnet werden können.

Dreiecke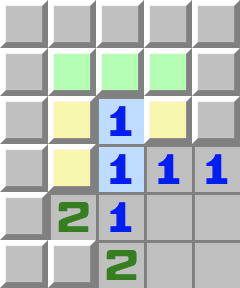

	B T1 Betrachten Sie die untere 1. Sie berührt die drei gelben Zellen, von denen deshalb genau eine eine Mine ist. Betrachten Sie nun die obere 1. Sie berührt ebenfalls die drei gelben Zellen, hat also bereits eine Mine, weshalb die übrigen grünen Zellen geöffnet werden können.
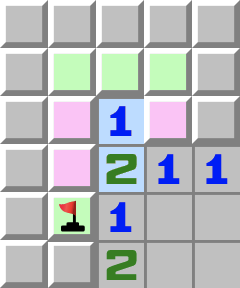	B T2 Betrachten Sie die lila Zellen. Sie enthalten höchstens eine Mine, da sie die 1 berühren. Betrachten Sie nun die 2. Wenn die lila Zellen höchstens eine Mine enthalten, dann muss das übrige grüne Feld der 2 eine Mine sein. Wenn Sie dort die Mine setzen, folgt daraus, dass in den lila Zellen eine Mine sein muss. Die 1 hat damit also eine Mine und die übrigen drei grünen Zellen können geöffnet werden.
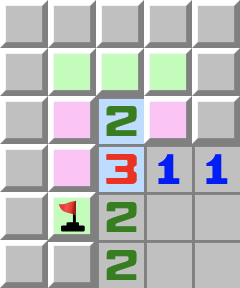	B T3 Betrachten Sie die lila Zellen. Sie enthalten höchstens zwei Minen, da sie die 2 berühren. Betrachten Sie nun die 3. Wenn die lila Zellen höchstens zwei Minen enthalten, dann muss das übrige grüne Feld der 3 eine Mine sein. Wenn Sie dort die Mine setzen, folgt daraus, dass in den lila Zellen zwei Minen sein müssen. Die 2 hat damit also zwei Minen und die übrigen drei grünen Zellen können geöffnet werden.
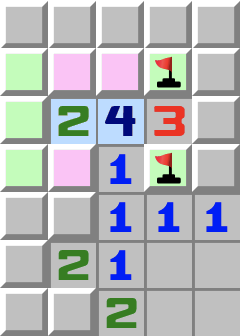	B T4 Betrachten Sie die lila Zellen. Sie enthalten höchstens zwei Minen, da sie die 2 berühren. Betrachten Sie nun die 4. Wenn die lila Zellen höchstens zwei Minen enthalten, dann müssen die übrigen grünen Felder der 4 zwei Minen sein. Wenn Sie dort die Minen setzen, folgt daraus, dass in den lila Zellen zwei Minen sein müssen. Die 2 hat damit also zwei Minen und die übrigen drei grünen Zellen können geöffnet werden.
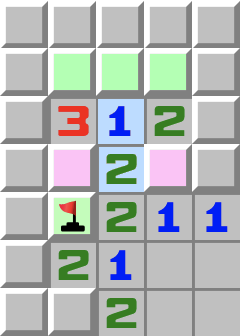	B T5 Betrachten Sie die lila Zellen. Sie enthalten höchstens eine Mine, da sie die 1 berühren. Betrachten Sie nun die 2. Wenn die lila Zellen höchstens eine Mine enthalten, dann muss das übrige grüne Feld der 2 eine Mine sein. Wenn Sie dort die Mine setzen, folgt daraus, dass in den lila Zellen eine Mine sein muss. Die 1 hat damit also eine Mine und die übrigen drei grünen Zellen können geöffnet werden.

Hochkomplexe Muster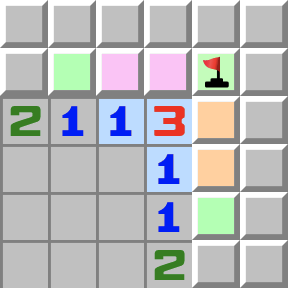

	B 1–3–1 Ecke Betrachten Sie die lila Zellen. Sie enthalten höchstens eine Mine, weil sie die 1 berühren. Betrachten Sie nun die orangen Zellen. Sie enthalten ebenfalls höchstens eine Mine. Betrachten Sie nun die 3. Die lila und orangen Zellen enthalten maximal zwei Minen, weshalb die dritte Mine in der Zelle in der Ecke sein muss. Die 3 hat noch zwei Minen übrig. Eine muss in den lila Zellen sein und die andere in den orangen Zellen. Deshalb können die übrigen beiden grünen Zellen keine Minen enthalten und geöffnet werden.
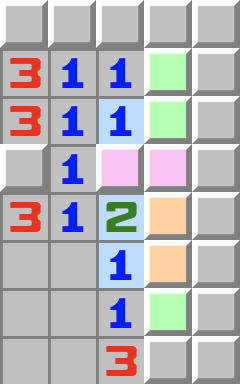
	B 2–2–2 Ecke Betrachten Sie die lila Zellen. Sie können nicht beide keine Mine enthalten, weil dadurch die 2 zu wenig Minen hätte. Deshalb enthalten sie mindestens eine Mine. Betrachten Sie nun die orangen Zellen. Sie können nicht beide keine Mine enthalten, weil dadurch die 2 zu wenig Minen hätte. Deshalb enthalten sie mindestens eine Mine. Betrachten Sie nun die 2 in der Ecke. Die lila und orangen Zellen enthalten jeweils mindestens eine Mine, wodurch die 2 in der Ecke bereits alle ihre Minen hat und weshalb die übrige Zelle in der Ecke geöffnet werden kann. Da in den lila und orangen Zellen jeweils eine Mine sein muss, kann die Zelle in der Ecke geöffnet werden und die beiden anderen Minen folgen.
	B 1>2<1 Betrachten Sie die lila Zellen. Sie enthalten höchstens eine Mine, weil sie die 1 berühren. Betrachten Sie nun die orangen Zellen. Sie enthalten ebenfalls höchstens eine Mine, weil sie eine 1 berühren. Betrachten Sie nun die 2. Die erste Mine muss in den lila Zellen sein und die zweite in den orangen Zellen. Deshalb können alle übrigen grünen Zellen geöffnet werden.
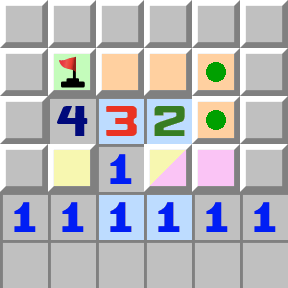	B T-Muster Die linke 1 berührt die beiden gelben Zellen, die deshalb genau eine Mine enthalten. Die rechte 1 berührt die beiden lila Zellen, die deshalb ebenfalls genau eine Mine enthalten. Die zwei berührt ebenfalls die beiden lila Zellen, weshalb die übrigen orangen Zellen ebenfalls genau eine Mine enthalten. Betrachten Sie nun die 3. Die gelben und orangen Zellen enthalten zusammen höchsten zwei Minen, weshalb die übrige dritte Mine in der Zelle in der Ecke sein muss. Betrachten Sie die 3 erneut. Die erste Mine ist in der Ecke, die zweite Mine ist in den unteren beiden Zellen, weshalb die dritte Mine in den übrigen beiden orangen Zellen ist. Daraus folgt, dass die beiden mit grünen Kreisen markierten orangen Zellen geöffnet werden können.
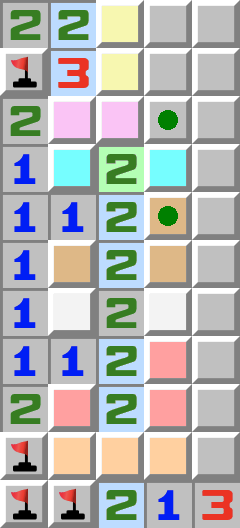	B Abhängigkeitsketten Üblicherweise können lange Abhängigkeitsketten gelöst werden, indem von beiden Seiten aus vorgegangen wird. Beginnen wir zuerst von oben. In den gelben Zellen ist genau eine Mine. In den lila Zellen ist genau eine Mine. Nun gehen wir von unten aus vor. In den orangen Zellen ist genau eine Mine. In den roten Zellen ist genau eine Mine. In den weißen Zellen ist genau eine Mine. In den braunen Zellen ist genau eine Mine. In den hellblauen Zellen ist genau eine Mine. Betrachten Sie nun die grüne 2. Die erste Mine muss in den lila Zellen sein, die zweite Mine muss in den hellblauen Zellen sein. Deshalb können die mit grünen Kreisen markierten Zellen geöffnet werden.

Letzte Züge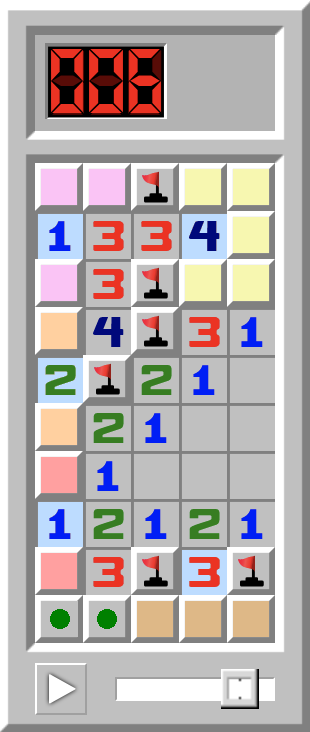

B Minen zählen Wenn das Spielfeld fast gelöst ist, können leere Zellen anhand der übrigen Minen gefunden werden: In den gelben Zellen sind zwei Minen. In den lila Zellen ist eine Mine. In den orangen Zellen ist eine Mine. In den roten Zellen ist eine Mine. In den braunen Zellen ist eine Mine. Die farbig markierten Zellen enthalten insgesamt sechs Minen, genauso viel wie übrig sind. Deshalb können die mit grünen Kreisen markierten Zellen geöffnet werden.

B Kombinationen In seltenen Fällen kann es erforderlich sein, alle möglichen Kombinationen durchzugehen: Wählen Sie eine beliebige Zelle. Zum Beispiel die gelbe Zelle. Prüfen wir, ob dort eine Mine sein kann. Falls die gelbe Zelle eine Mine ist, dann benötigt die restliche Lösung sechs Minen. Die Kombination ist nicht möglich, weil nur noch fünf Minen übrig sind. Deshalb kann die gelbe Zelle keine Mine sein und kann geöffnet werden.