| |
Un schéma (en anglais “pattern”) est une combinaison courante de nombres de mines offrant une seule solution. En mémorisant les schémas, vous réduirez votre temps de réflexion.
Schémas de base | B1- Si un nombre touche le même nombre de cases,
- alors ces cases sont toutes des mines.
| 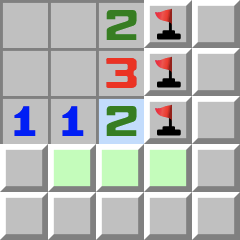 | B2- Si un nombre touche déjà le même nombre de drapeaux,
- alors toutes les autres cases adjacentes peuvent être ouvertes.
| 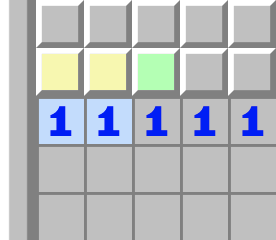 | 1–1- Regardez le 1 de gauche près du bord.
- Il touche les deux cases jaunes, donc l’une des deux est une mine.
- Regardez maintenant le 1 à sa droite.
- Il touche lui aussi les deux cases jaunes, donc il a déjà sa mine et la troisième case, en vert, peut être ouverte.
| 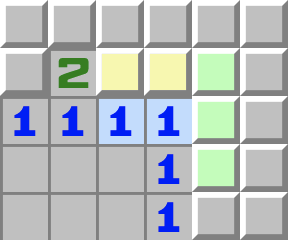 | 1–1+- Regardez le 1 surligné en bleu de gauche.
- Il touche les deux cases jaunes, donc l’une des deux est une mine.
- Regardez maintenant le 1 surligné en bleu de droite.
- Il touche lui aussi les deux cases jaunes, donc il a déjà sa mine et toutes les cases restantes peuvent être ouvertes.
| 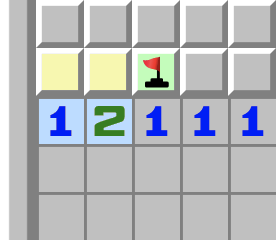 | 1–2- Regardez le 1 surligné en bleu.
- Il touche les deux cases jaunes, donc l’une des deux est une mine.
- Maintenant regardez le 2.
- Sa première mine est l’une des deux cases jaunes, donc sa deuxième mine est dans la troisième case.
| 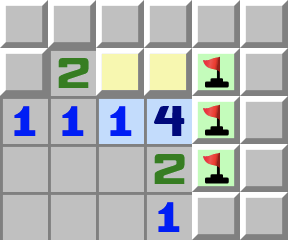 | 1–2+- Regardez le 1 surligné en bleu.
- Il touche les deux cases jaunes, donc l’une des deux est une mine.
- Maintenant regardez le 4.
- Sa première mine est l’une des deux cases jaunes, donc les trois cases restantes sont forcément toutes des mines.
| 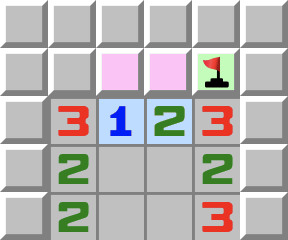 | 1–2CVersion classique du schéma 1–2: - Regardez les cases roses. Que peut-on dire d’elles ?
- Elles ne peuvent être des mines toutes les deux à la fois, cela dépasserait les capacités du 1. Elles contiennent au maximum une mine.
- Maintenant regardez le 2.
- Si une seule des cellules roses est une mine, alors il y a une mine dans l’autre case touchant le 2.
| 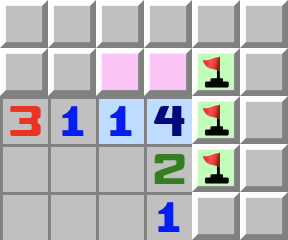 | 1–2C+- Regardez les cases roses. Que peut-on dire d’elles ?
- Elles ne peuvent être des mines toutes les deux à la fois, cela dépasserait les capacités du 1. Elles contiennent au maximum une mine. Maintenant regardez le 4.
- Maintenant regardez le 4.
- Si une seule des cellules roses est une mine, alors les trois autres cases touchant le 4 sont des mines.
| 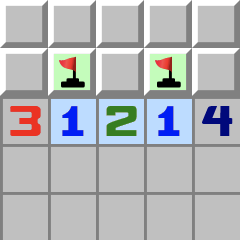 | 1–2–1Le schéma 1–2–1 a une unique solution. En fait il s’agit de la combinaison de deux schémas 1–2: - Appliquez le schéma 1–2 à partir de la gauche.
- Appliquez le schéma 1–2 à partir de la droite.
- Voilà le résultat final.
| 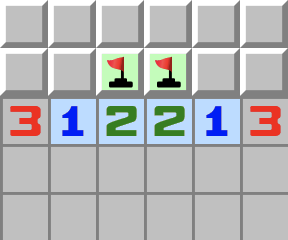 | 1–2–2–1Le schéma 1–2–2–1 a une unique solution. C’est aussi la combinaison de deux schémas 1–2: - Appliquez le schéma 1–2 à partir de la gauche.
- Appliquez le schéma 2–1 à partir de la droite.
- Et voilà le résultat final.
|
Réductions | 1–1R- Le 2 surligné en bleu se réduit en 1, puisqu’il a déjà une mine à sa gauche.
- Le 4 se réduit aussi en 1, puisqu’il a déjà trois mines.
- Donc, le 2–4 devient un schéma 1–1 et la troisième case, en vert, peut être ouverte.
| 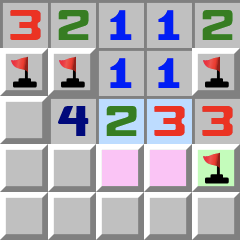 | 1–2R- Le 2 se réduit en 1, puisqu’il a déjà une mine à sa gauche.
- Le 3 surligné en bleu lui devient 2, puisqu’il a déjà une mine.
- Donc le 2–3 devient un schéma 1–2 et la troisième case, en vert, peut être ouverte.
| 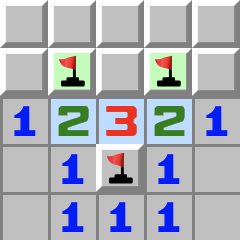 | 1–2–1R- Le schéma 2–3–2 se réduit à un schéma 1–2–1.
|
Trous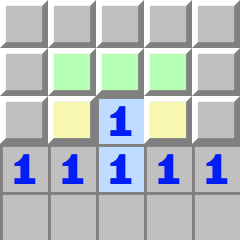 | H1- Regardez le 1 central du bas.
- Il touche les deux cases jaunes, donc l’une des deux est une mine.
- Maintenant regardez le 1 du haut.
- Lui aussi touche ces deux cases jaunes, donc toutes les cases supérieures en vert peuvent être ouvertes.
|  | H2- Regardez le 1 central du bas.
- Il touche les deux cases jaunes donc l’une des deux est une mine.
- Maintenant regardez le 1 du haut.
- Lui aussi touche ces deux cases jaunes donc toutes les cases supérieures en vert peuvent être ouvertes.
| 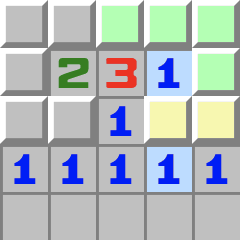 | H3- Regardez le 1 du bas surligné en bleu.
- Il touche les deux cases jaunes, donc l’une des deux est une mine.
- Regardez maintenant le 1 du dessus.
- Lui aussi touche ces deux cases jaunes, donc il a déjà sa mine et toutes les cases adjacentes en vert peuvent être ouvertes.
|
Triangles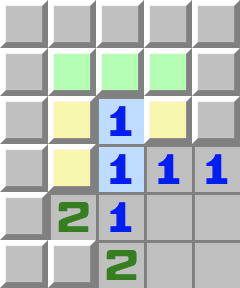 | T1- Regardez le 1 surligné en bleu du bas.
- Il touche les trois cases jaunes, donc l’une d’entre elles est une mine.
- Regardez maintenant le 1 surligné du haut.
- Il touche aussi les trois cases jaunes, donc il a déjà parmi elles sa mine, donc les trois cases vertes au-dessus peuvent être ouvertes.
| 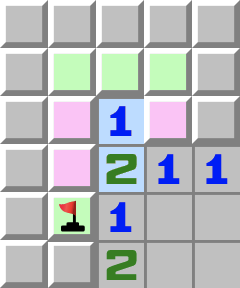 | T2- Regardez les cases roses.
- Une et une seule de ces trois est une mine puisqu’elles touchent le 1 surligné en bleu.
- Regardez maintenant le 2 surligné en bleu.
- Si les cases roses contiennent une mine, alors la deuxième mine se trouve dans la dernière case adjacente.
- Si vous posez le drapeau, vous pouvez voir qu’une mine se trouve dans les cases roses. Donc le 1 surligné de bleu a déjà sa mine et les trois cases vertes au-dessus peuvent être ouvertes.
| 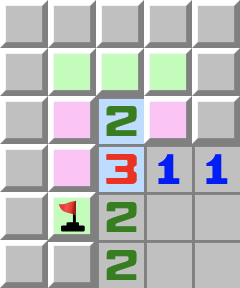 | T3- Regardez les cases roses.
- Elles contiennent au maximum deux mines puisqu’elles touchent toutes les trois le 2 surligné en bleu.
- Maintenant regardez le 3.
- Si les cases roses contiennent au maximum deux mines, alors il doit y avoir une mine dans la dernière case adjacente disponible.
- Si vous placez le drapeau, vous voyez que deux mines se trouvent dans les cases roses. Donc le 2 surligné en bleu a déjà ses mines et les trois cases vertes au-dessus peuvent être ouvertes.
| 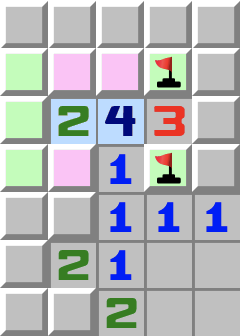 | T4- Regardez les cases roses.
- Elles contiennent au maximum deux mines, puisqu’elles touchent toutes le 2 surligné en bleu.
- Maintenant regardez le 4.
- Si les cases roses contiennent au plus deux mines, alors on trouve deux mines dans les cases adjacentes restantes.
- Si vous placez les drapeaux, vous voyez que deux mines se trouvent dans les cases roses. Donc le 2 surligné en bleu a déjà ses mines et les trois cases vertes à gauche peuvent être ouvertes.
| 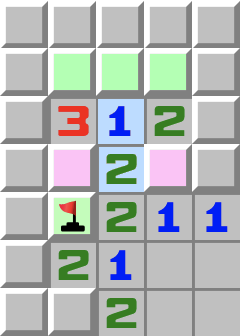 | T5- Regardez les cases roses.
- Elles contiennent au maximum une mine puisqu’elles touchent toutes les deux le 1 surligné en bleu.
- Regardez maintenant le 2 surligné.
- Si les cases roses contiennent au maximum une mine, alors une mine doit se trouver dans la dernière cases adjacente en bas à gauche.
- Si vous placez le drapeau, vous voyez qu’une mine se trouve dans l’une des deux cases roses. Donc le 1 a déjà sa mine et les trois cases vertes au-dessus peuvent être ouvertes.
|
Schémas complexes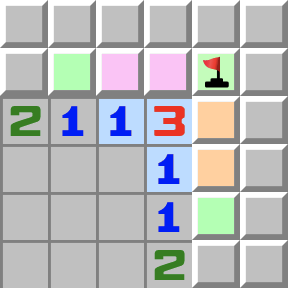 | Angle 1–3–1- Regardez les cases roses.
- Elles contiennent une et une seule mine, puisqu’elles touchent le 1.
- Regardez maintenant les cases oranges.
- Elles aussi contiennent une et une seule mine puisqu’elles aussi touchent un 1.
- Maintenant regardez le 3.
- Les cases roses et oranges contiennent chacune une mine, cela en fait deux, donc la troisième mine se trouve dans la seule case adjacente libre, à l’angle.
- Deux mines manquent encore au 3. L’une d’elles se situe dans les cases roses, l’autre dans les cases oranges. Donc l’angle 1–3–1 a une unique solution.
|  | L’angle 2–2–2- Regardez les cases roses.
- Elles ne peuvent être vides, il manquerait une mine au 2 surligné. Donc elles contiennent au moins une mine
- Regardez maintenant les cases oranges.
- Elles ne peuvent être vides, il manquerait une mine au 2 surligné. Donc elles contiennent au moins une mine.
- Regardez maintenant le 2 à l’angle.
- Les cases oranges et roses contiennent au moins deux mines en tout, donc ce 2 a déjà ses mines et la case à l’angle peut être ouverte.
- Une mine se trouve dans les cases roses, et la seconde dans les cases oranges. Donc, l’angle 2–2–2 corner a une unique solution.
| 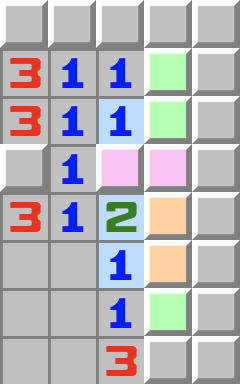 | 1>2<1- Regardez les cases roses.
- Elles contiennent au maximum une mine puisqu’elles touchent le 1 surligné.
- Regardez maintenant les cases oranges.
- Elles aussi contiennent au plus une mine puisqu’elles aussi touchent un 1.
- Maintenant regardez le 2.
- Sa première mine se situe dans les cases roses, et sa deuxième dans les cases oranges. Donc, toutes les autres cases adjacentes aux 1 surlignés peuvent être ouvertes.
| 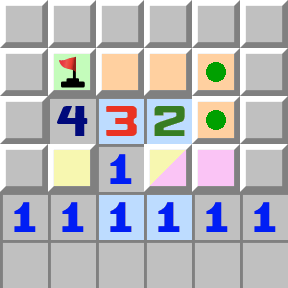 | Le schéma T- Le 1 surligné de gauche touche les deux cases jaunes, donc elles contiennent une mine.
- Le 1 surligné de droite touche les deux cases rose, donc l’une des deux est aussi une mine.
- Le 2 touche les deux cases roses, donc une mine et une seule se trouve parmi les cases oranges.
- Maintenant regardez le 3.
- Les cases oranges et jaunes contiennent deux mines en tout, la troisième mine se trouve donc forcément dans la seule case adjacente restante, à l’angle.
- Regardez le 3 de nouveau. La première mine est à l’angle, la seconde parmi les deux du bas, donc la troisième est l’une des deux cases oranges restantes. Les cases marquées d’un point vert peuvent donc être ouvertes.
| 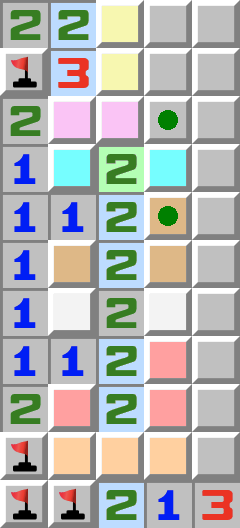 | Chaîne de dépendanceD’habitude les longues chaînes de dépendance se résolvent en analysant à partir des deux côtés. - Commençons l’analyse par le haut.
- Une mine se trouve dans les cases jaunes.
- Une mine se trouve dans les cases roses.
- Analysons maintenant à partir du bas.
- Une mine se trouve dans les cases oranges.
- Une mine se trouve dans les cases rouges.
- Une mine se trouve dans les cases blanches.
- Une mine se trouve dans les cases marrons.
- Une mine se trouve dans les cases turquoises.
- Regardez maintenant le 2 encadré des cases turquoises.
- Sa première mine est l’une des deux cases roses, sa deuxième mine l’une des deux cases turquoises. Donc les cases marquées d’un point vert peuvent être ouvertes.
|
Derniers coups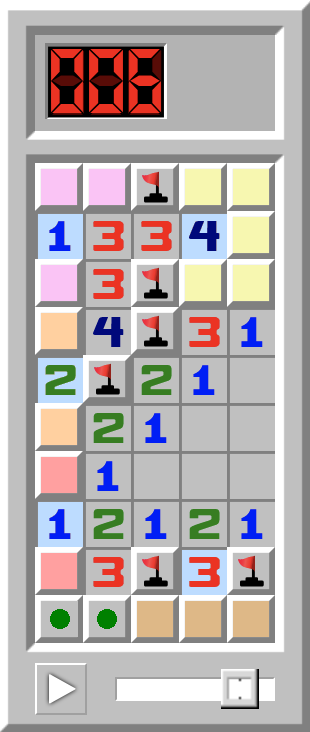 | Décompte des minesQuand arrive la fin du tableau, vous pouvez déterminer des cases libres en comptant le nombre de mines restantes: - Deux mines se trouvent parmi les cases jaunes.
- Une mine se trouve parmi les cases roses.
- Une mine se trouve parmi les cases oranges.
- Une mine se trouve parmi les cases rouges.
- Une mine se trouve parmi les cases marrons.
- Les cases colorées contiennent six mines au total, exactement le nombre de mines restantes. Les cases marquées d’un point vert peuvent donc être ouvertes.
|  | CombinaisonsDans quelques rares situations, il peut être nécessaire de recenser les combinaisons possibles. - Choisissez une case de façon arbitraire. Par exemple ici la case jaune.
- Vérifions s’il peut s’agir d’une mine.
- Si une mine se trouve dans la case jaune, alors la solution finale réclame six drapeaux. Cette combinaison est impossible puisqu’il ne reste que cinq mines à pourvoir.
- Donc, la case jaune n’est pas une mine et peut être ouverte.
|
|